An aside on two jokes about silly functions and what we can learn from them

Earlier this week I wrote a post about disambiguating the word function. This is not part 2 of that post - which is something I am still working on.

The post ended by taking two examples of C programs which print a 12x12 multiplication table.

The first works by iterating over every required entry in the table, and carrying out the appropriate multiplication.

int main(void)
{
    int i, j, n = 12;

    for (j = 1; j <= n; j++) printf("%3d%c", j, j != n ? ' ' : '\n');
    for (j = 0; j <= n; j++) printf(j != n ? "----" : "+\n");

    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++)
            printf(j < i ? "    " : "%3d ", i * j);
                printf("| %d\n", i);
        }

    return 0;
}

The second is both kind of silly and kind of clever at the same time. Instead of actually multiplying any numbers together it has just memorised all the lines of the 12x12 table and outputs them one by one:

#include <stdio.h>

int main(void)
{
    printf("  1   2   3   4   5   6   7   8   9  10  11  12\n");
    printf("------------------------------------------------+\n");
    printf("  1   2   3   4   5   6   7   8   9  10  11  12 | 1\n");
    printf("      4   6   8  10  12  14  16  18  20  22  24 | 2\n");
    printf("          9  12  15  18  21  24  27  30  33  36 | 3\n");
    printf("             16  20  24  28  32  36  40  44  48 | 4\n");
    printf("                 25  30  35  40  45  50  55  60 | 5\n");
    printf("                     36  42  48  54  60  66  72 | 6\n");
    printf("                         49  56  63  70  77  84 | 7\n");
    printf("                             64  72  80  88  96 | 8\n");
    printf("                                 81  90  99 108 | 9\n");
    printf("                                    100 110 120 | 10\n");
    printf("                                        121 132 | 11\n");
    printf("                                            144 | 12\n");

    return 0;
}

There are a lot of jokes that get passed around the internet among programmers about similarly silly functions, for example this one which generates a "random" number:

...or this one which checks whether an input is even or odd.

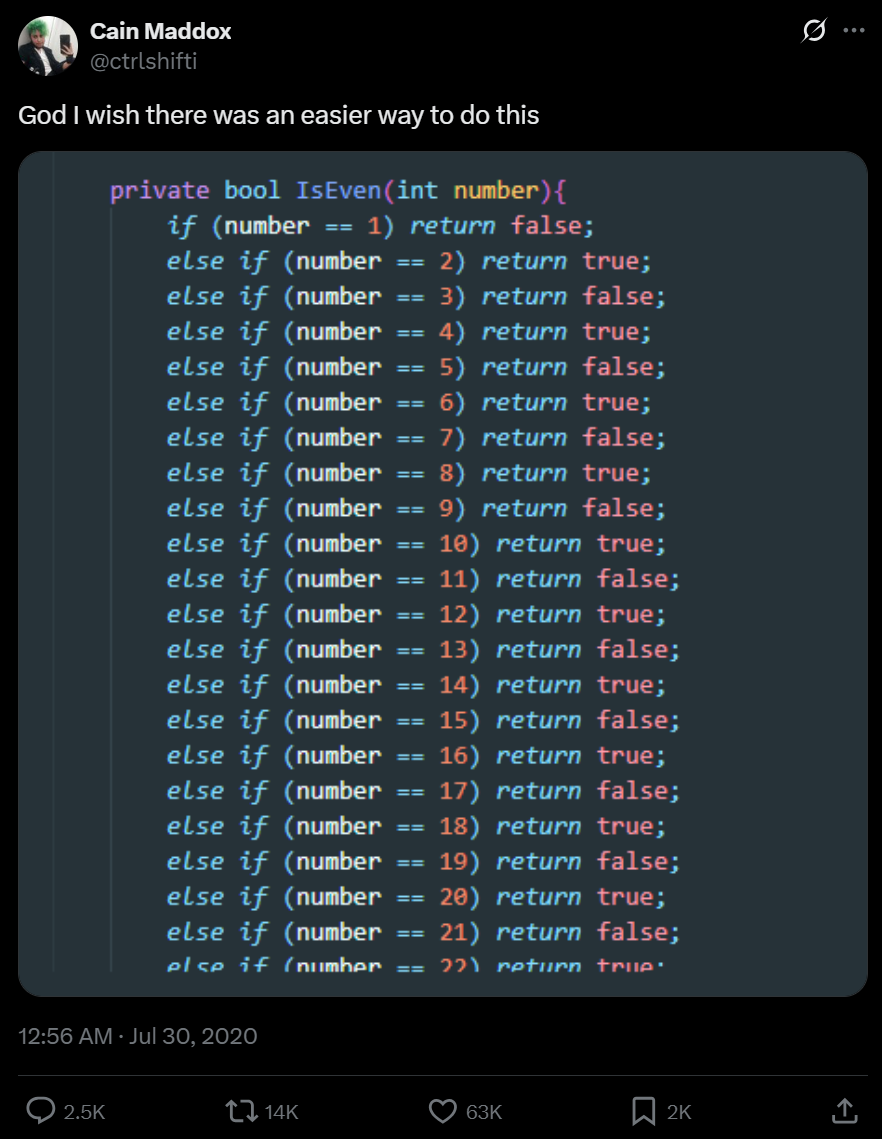
Let's talk through these two examples in turn, then back up and talk about what makes our original two C programs different from one another.

In the case of getRandomNumber() - the first time you use it (assuming you haven't read the source code) you probably don't notice that anything is up. After a few more times, you quickly discover that it is just returning the number 4 each time it's run, which makes it kind of useless as a program for generating random numbers.

IsEven() is more interesting. Using the language of my earlier post it is functionally identical to the usual method for testing if a natural number is even (computing i mod 2) in both the teleological and set theoretic senses. The small catch is, that a fully general version of program described in the tweet appears to be impossible to write. More precisely you might struggle to write it in a finite number of lines, because there are infinitely many possible numbers which you could run an IsEven function on.

There is a way around this though, which is to take advantage of the fact that computer hardware is finite, and so for any given variable there is generally¹ a maximum numerical value it is allowed to represent. In the case of the screenshot it is probably something like 2,147,483,647. You could list out all 2,147,483,647 cases and your program really would be identical (at least both teleologically and set-theoretically) to a program which checks the remainder when dividing by two and only returns True if that remainder is zero.

Our two 12x12 multiplication table programs are another case of this. One way you might think they are different is that the program that actually carries out the multiplications can be extended to the case of generating any NxN multiplication table. However, just as with IsEven, for any finitely-bounded set of inputs you can always make adjustments to extend the silly program to have the same behaviour as the one which actually does the multiplications. The way they actually differ remains opaque so long as you restrict yourself to just looking at their inputs and outputs. This sets the scene to discus some other meanings which the word "function" can have.

Asking "how?" rather than "what?" or "why?"

Sometimes when we talk about something's function we are talking about the procedure it is carrying out, for example we might look at two things that share the same behaviour and purpose and still ask: "do they function the same way?" and what we are asking is not a question of what they do or why they do it but how they do it.

It's clear by looking at their source code in the case of the two programs above the answer to this question is that they are doing quite different things to arrive at the same answer. At the same time - it's not the case that every two programs with different source code are functionally different. Examples of changes you could make to a function's source code which don't affect how they function include, for example:

• changing all the variable names
• swapping the order of arguments of commutative operators
• adding or removing comments
• reformatting whitespace

In the case of our two C programs, what we want to be able to say is something about how the internal logic of one program can generalise to infinitely many cases, while the other has been thrown together "ad hoc" from many individual cases. I will be talking about approaches to do this in my upcoming part 2 post about disambiguating the word "function".